|
Phisics/StreetsDemo.zip
| |
[Главная
страница] [Физики ] [Не знаю]

|
|
|
|
Как я уже написал в предисловии на странице Физики, данный пример явился
результатом задания по сжатию базы данных,
содержащей названия улиц. Маркетинговая
компания использовала эти данные в своих
исследованиях по опросам аудитории СМИ (средств
массовой информации). Названия улиц фигурировали
в адресах респондентов, участвующих в опросах. В
такой сфере деятельности особое внимание
уделяется достоверности данных, а система сбора
данных о респондентах такова, что эти данные
переводятся в электронный вид самыми разными
способами, различными людьми в различных городах
России. Поэтому проблема повторяемости и даже
искажения данных стояла достаточно остро.
Очень быстро (за два-три дня) был
придуман алгоритм, а по нему сделана программка,
позволяющая группировать названия улиц по
степени их "похожести" на указываемое
"эталонное" название. Саму программку
вместе с примером базы данных можно загрузить отсюда, а пока внешний вид
программного интерфейса можно увидеть на
рисунке ниже:
|
|
|
 |
|
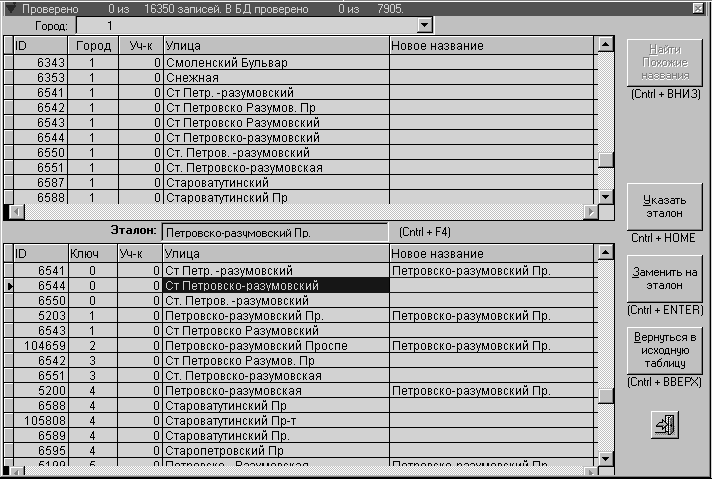
Теперь необходимо привести пояснения, как это
работает.Экран состоит из двух таблиц с
одинаковыми полями. На самом деле в них
содержатся записи из одной и той же таблицы.
Только в верхнем списке улицы (записи)
расположены по алфавиту, а в нижнем - в порядке
убывания их "похожести" на эталонное
название. Эталонное название можно увидеть в
специально отведенном для него текстовом поле с
надписью "Эталон:" (оно расположено между
двумя этими таблицами).
Различный порядок предъявляемых
записей иллюстрируется полем с идентификатором
записи (ID). Поле "Ключ" в нижней таблице - это
и есть "коэффициента похожести" на эталон.
В самом верху окна надо выбрать город
из списка городов. Это для того, чтобы похожие
улицы из других городов не мешали. После чего в
верхнем списке будут видны улицы только из этого
города.
С правой стороны расположены кнопки,
управляющие действиями пользователя. Сначала
активна только самая верхняя из них.
 | Выбрав в верхнем списке улицу, для которой мы
хотим найти похожие названия в Базе Данных,
нажимаем кнопку "Найти похожие названия"
запускается процедура расчета "ключа", по
значению которого упорядочиваются записи в
нижнем списке. Название появится в текстовом
поле "Эталон". Одновременно станут
доступными кнопки: "Указать эталон" и
"Вернуться в исходную таблицу", а
нажатая "Найти похожие названия" останется
недоступной. |
Теперь можно листать нижний список и выбирать
улицы, с подходящими названиями:
 | Нажатием кнопки "Указать эталон" можно
изменить сам эталон на текущее значение в нижнем
списке. Кроме того текст эталона допускает
корректировку. Кроме того еще эта кнопка
активирует кнопку "Заменить на эталон". |
 | Затем нужно в нижнем списке прочитать первые
10-20 записей и решить, какие из них должны
соответствовать эталону, и для каждой такой
записи нажать кнопку "Заменить на эталон".
После этого в соседнем поле "Новое название"
появится эталонное название улицы. Тем самым,
записи, у которых это поле заполнено следует
считать отклассифицированными. Для них больше не
нужно делать ничего. Решение о том, что делать в
последствии со старым названием и заменять ли
его на новое, принимает администратор Базы
Данных. |
 | Кнопка "Вернуться в исходную таблицу"
служит для того, чтобы снова переключиться в
верхний список и начать поиск для нового эталона.
Одновременно вовь активируется кнопка "Найти
похожие названия", а кнопки для работы с
эталоном становятся недоступными. |
Эту процедуру можно продолжать до тех пор, пока
во всех запися поле "Новое название" не
станет заполненным.
Вы можете сами пополнить предлагаемую базу
данных по аналогии с уже имеющимися данными.
Программа предназначена для Visual Foxpro 5 и выше и
очень наглядно демонстрирует свойства алгоритма.
Несмотря на EXE-расширение, она запускается только
из интегрированной среды Visual Foxpro. Обязательно
прочитайте файл "Readme.txt" внутри архива.
(Правило формирования ключа и пример программы
помещены в следуещем параграфе). |
|
Правило формирования
коэффициента похожести.
Для тех, кто капельку знаком с теорией
кодирования и передачи информации сразу скажу
основную суть правила формирования ключа (т.е.
коэффициента похожести, а скорее, наоборот,
различия):
ключ формируется по правилу
Хэмминга.
Но это только основная суть правила, а вот об
остальных условиях - ниже.
 | К какой формулировке была сведена
задача? |
Задача была сведена к следующей формулировке:
Существуют текстовые строки, ограниченной длины.
Следует объединить их в группы так, чтобы в
каждой группе строки не сильно отличались друг
от друга.
В такой упрощенной формулировке постановка
является стандартной задачей кластеризации. Для
их решения разработано много автоматических
методов кластеризации. (Кстати один из таких
метов был разработан автором этих строк
собственноручно и использован в программе по
обработке топографических карт, помещенной на
этом же сайте на странице Физиков, см.
гиперссылку в начале этой страницы). Но в данной
ситуации овчинка не стоила выделки. Требовалось
что-нибудь проще, точнее, а главное раньше.
Поэтому я остановился на методе ручной
группровки текстовых строк вблизи предъявляемых
эталонов.
(Пользователи сами находят эталоны, которые
будут образовыввать группы-кластеры и сами же
отбирают похожие на эталон текстовые строки.
Только претенденты, похожие на выбранный эталон
подбирались программой автоматически. Как это
выглядит для пользователя, я описал выше).
 | Что означает фраза "текстовая
строка похожа на эталон"? |
Как говорится, спасибо за вопрос.
Для ответа на него следует обратиться к
теории метрических пространств.
Рассмотрим множество, состоящее из
всевозможных текстовых строк ограниченной
длины. Это можество будет у нас являться
пространством, точками которого являются
текстовые строки (т.е. одна строка - это одна
точка, разные строки - разныые точки, одинаковые
строки - одна и та же точка).
Мы хотим научиться как-нибудь измерять
расстояние между точками этого пространства.
Тогда и можно будет говорить о "похожести":
чем ближе точки, тем похожей соответствующие
текстовые строки.
Определение. Метрическим пространством
называется множество, для которого существует
функция от двух переменных, заданная на парах
точек этого множества, и обладающая свойствами
расстояния.
В этом случае про значение функции на паре точек
можно говорить, что оно является расстоянием
между этими двумя точками множества. При этом
можно рисовать точки на бумаге, например, и не
задумываться о природе множества. А саму функцию
можно называть расстоянием , или метрикой.
(Какими свойствами обладает расстояние, нас и вас
учили еще в пятом классе: неравенство
треугольника и т.д.)
Для рассматриваемого случая в качестве метрики
была выбрана идея Хэмминговой метрики.
Применяться она должна следующим образом:
Если текстовые строки имеют одинаковую длину, то
расстояние между ними - это количество
несовпадающих символов.
Если текстовые строки имеют разнуюую длину, то
расстояние между ними - это чуть сложнее.
Для определенности в этом случае следует
считать, что все строки имеют одинаковую длину
(вспомним, ведь их длина ограничена каким-то
числом, вот оно и будет длиной всех строк, а
оставшуюся часть, где реальная строка кончается,
можно заполнить например символом ACII=0). Тогда
длина таких двух строк расчитывается как в
первом случае.
На этом можно было бы поставить точку. Но...
Оказалось, что можно улучшить алгоритм,
рассматривая несколько иное метрическое
пространство, учитывающее особенности, оторые
влияли на ошибки при вводе текстов. Например, при
вводе соседние буквы иногда переставляются
местами, или нажимается соседняя клавиша, или
дважды одна и та же буква, или случайно
прпускается какая-то буква и т.п. Я рассуждал так.
Представьте, что слово один раз ввелось
правильно, а во второй раз пропустили первую
букву. В результате вся строка сдвинулась
влево по сравнению с первой. Если применять
правило сравнения в лоб, то эти два слова будут
несовпадать в кадой позиции, и значи очень сильно
отличаться друг от друга. Хотя на самом деле
расстояние между ними хотелось бы получить
минимальным.
К тому же латинские буквы вообще можно
игнорировать, если их одна-две. Цифры и знаки
пунктуации в названиях улиц также можно не
рассматривать и т.п. Тем самым размер текстоой
строки уменьшается.
Исходя из этих соображений я реализовал
следующий алгоритм:
Берем строки длиной в 256 символов. Они и будут у
нас точками метрического постранства. Каждой
позиции соответствует ASCII код с номером позиции.
Отсчет позиций, поэтому ведем от 0 до 255.
При сравнении полученных строк игнорируем
позиции, соответствующие в ASCII кодировке всей
нижней половине таблицы. Т.о. остаются только
верхние 128 символов. Среди них игнорируем символы
псевдографики, нижний и верхний регистр будем
считать совпадающими. Остаются только 32 буквы
русского алфавита. Это и будет длина текстовой
строки. Повторы букв в словах не учитываем. Легко
видеть, как подобное построение можно
распространить и на другие виды кодировок.
Расстояние между строками и этолоном
рассчитывается так:
Берем эталон. Если в нем присутствует буква
"А", заносим "1" в соответствующюю
позицию. Если в нем присутствует буква "Б",
заносим "1" в соответствующюю позицию. Если в
нем присутствует буква "В", заносим "1"
... Понятно? Остальные позиции заполняются нулями.
В результате будет сформирована строка из
"0" и "1".
Также поступаем со сравниваемой строкой.
В результате будет сформирована еще одно строка
из "0" и "1".
Расстояние между ними - это количество
отличающихся позиций.
Эта величина и отражена на рисунке в поле
"Ключ" в нижнем списке.
Теперь должно быть понятным, что листать нижний
список далеко вниз не имеет смысла. Если значение
ключа больше, например, 10, то названия улиц скорее
всего сильно не похожи друг на друга.
 | Почему пришлось что-то придумывать,
а не использовать встроенные функции языка? |
Потму, что несмотря на существование
встроенной функции в языке программирования, а в
данном случае это был Visual FoxPro v.5.0, и несмотря на
то, что это была русская версия, функция эта никак
не хотела работать с русским текстом. (Она и для
английского-то текста выдает только четыре
уровня отличий).
Уф! Легче было придумать, чем написать. Да еще
понятно ли?
Надеюсь, что в общих чертах я сумел ответить на
главные вопросы. Кто бы мог подумать, что за такой
невзрачной программкой может стоять целая
математическая теория. И даже не одна, а
несколько, на основе которых можно компоновать
бесконечное разнобразие алгоритмов обработки
текстов. Если остались вопросы, пишите, адрес
приведен в низу страницы. |
|

|
|
Предложения присылайте на poldom@mail.ru
© ТПА Эксперт, Москва, 1999 |
|
![]()
